Intellectual Background

About 100 years ago, one of the founders of modern formal logic, the American logician and philosopher of language Charles Saunders Peirce, expressed concerns regarding the traditional linear notation of formal logic. Thus, Peirce proposed an alternative system with a more graphical notation, called Existential Graphs (Peirce, 1933).

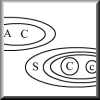
Whereas Venn diagrams are a well-known diagrammatic representation that can be used for categorical logic, Existential Graphs are a little-known diagrammatic representation that can be used for propositional, quantificational, and modal logic. Interestingly, in Existential Graphs one hardly uses any special symbols. For example, conjunctions (and's) are represented by the juxtaposition of parts (so no symbol is really used at all), and negations (not's) are represented by the "cut": an enclosing figure such as a circle, rectangle, or ellipse. As students of logic know, all other truth-functional operators can be expressed in terms of conjunctions and negations, and this is exactly what Existential Graphs does. Moreover, while normally a reduction in logical operators translates into an increase in the amount of work one has to do in logical inference, proofs in Existental Graphs are actually often quite a bit shorter than those using the traditional linear notation.

Peirce meant for his Existential Graphs to be "iconic", meaning that the nature of the representations should be reflective of their meaning. Thus, first of all, anything that is placed on the "Sheet of Assertion" is something that is being asserted as true, and this seems indeed very natural: whatever I write on the paper, I assert as being true. The user also immediately and intuitively grasps the fact that location is unimportant: whether something is in the top left corner or bottom right does not matter, and it is only by going inside or outside cuts that something of interest happens and the meaning of the representation changes. Cuts also provide a natural context for a certain collection of information, the juxtaposition of which is immediately grasped as one big conjunction, and thus as a kind of "scenario". Indeed, Existential Graphs have the very appealing feature of supporting a syntactic proof-theoretic, as well as a more semantic model-theoretic, reading and use (van Heuveln, 2006).

In fact, through its notation, Existential Graphs eliminates some unfortunate artifacts as introduced by the traditional linear notation. For example, since there is no order imposed on the component parts, there is no such thing as a difference between P & Q and Q & P: both statements would be represented in Existential Graphs the same way, namely as the juxtaposition of two subgraphs P and Q. Indeed, there is no one-to-one mapping between Existential Graphs and the more traditional symbolic notations, which provides Existential Graphs with yet another advantage: the graphs for ~(P & ~Q), ~P v Q, and P->Q are all the same, capturing important logical equivalences that in the traditional system need to be memorized.

An additional interesting feature of Existential Graphs is that the nature of proofs in a subtly different way as compared to traditional systems. In traditional formal logic, a proof is a sequence of statements, that one writes after (or under) each other. However, in Existential Graphs, all of the inference rules of the system require one to either add or remove parts to or from a single graphical notation. Thus, a proof in Existential Graphs is the successive transformation of one graph, representing the given information, to another, representing the inferred information. Indeed, one transforms, rather than rewrites. Crudely put: a proof in Existental Graphs is a movie!

Moreover, when doing proofs in Existential Graphs, one often finds oneself pulling relevant information into a certain context, combining it with other parts present in that context, and removing those parts that aren't useful or that were usefiul but "done with". This seems to be a very natural and healthy way to conceptualize the reasoning process.

Finally, the cuts provide a natural way to divide and conquer, as they naturally break the graph down into sub problems, or possible scenarios that can be processed in parallel. This reduces the user's mental workload because the user only needs to keep a subset of relevant information in his/her working memory. It also opens the door for parallel processing: Peirce himself envisioned mutltiple users to be able to interact with the same graph, and there are some interesting possibilites for automated theorem proving here as well.

Despite all these obvious advantages, Existential Graphs are a surprisingly little known system within the logic community. It appears in only few articles and books, and there is no logic textbook that we know of that presents the system to the student. The system also has one big disadvantage, and that is that it does not naturally map onto English which, like the traditional symbolic notation, is a linear language. Indeed, for beginners of the system, it can be hard to express what the diagram is saying in words. However, with a little training, one actually quickly gets a lot better in this.

In fact, a different way of looking at the mismatch between Existential Graphs and English, is not to "blame" Existential Graphs, but to "blame: English (or any other natural language)! Indeed, one can speculate that if our natural means of comunication would have been visual (and thus diagrammatic), rather than the spoken word (and thus linear), we might have found Existential Graphs perfectly natural, and we would probably have found the linear notation of traditional logic not just alien, but also oddly inefficient. Imagine: if we would have evolved from the Teletubbies, communicating through the screens in our bellies, we might have been a lot smarter!

A final reason for the system not being used more is probably that the system is not well suited for paper and pencil. On paper, the physical transformations of existential graphs often quickly result in a mess, especially if one does has to change the size of a cut in order for it to contain more information, and particularly when one does not have a good eraser! Also, when one is done with the process, there is no history of the moves that one has made, unless one redraws the successive steps as separate graphs, which defeats part of the appeal of the system as discussed above.

However, with a good computer interface, none of this should be an obstacle: the computer can cleanly erase, resize, reorganize, and keep a history of successive moves. And, the interface can always provide one or more English-like readings of the graph or, if one wants, corresponding formal logic representations. A few computer programs for the use of Existential Graphs have been made, including some by Dr. Van Heuveln and his students. None of them have the kind of fluid interface yet that would allow one to truly explore the potential power of Existential Graphs, but with advancing technology and software we're getting closer and closer.

We are particularly interested in using multi-touch sensing technology, which would be a natural fit for Existential Graphs in many ways. For example, for the rule of iteration, which allows one to create or erase a copy of a part of a graph into or from another part of a graph, one could use one hand to indicate the original, while the other can place or remove the copy. In general, one can use one hand to perform a manipulation, while the other indicates its justification, an operation that is of course central to doing loigic proofs, whether that be in Existential Graphs or any other system of logic. Most interestingly is that hand-movements to pull in, combine, and throw away information will feel completely natural and intuitive. Indeed, we also would like to explore using gesturing technology, like the Kinect, to drive such "embodied reasoning" processes.