Critical Wisdom - Deductive Reasoning

4.1 Deductive Reasoning -- Validity and Soundness

Now that we know something about arguments, we will look at a very narrow variety of arguments that are notable for their seemingly “precise nature.” Deductive arguments are examples of a kind of reasoning that purports to be conclusive reasoning. If we have a deductive argument that has both “good form” and “true content,” then we have an argument such that the truth of the premises guarantees the truth of the conclusion. Here is a simple one:

We can represent this argument as follows:

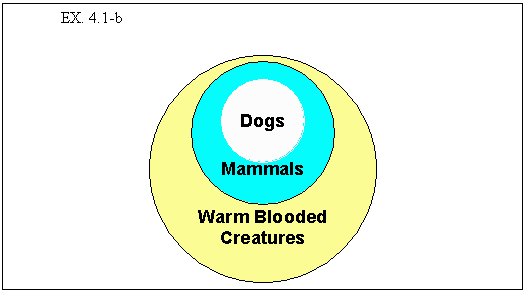
Note that, as the argument states, if it is true that all mammals are warm blooded creatures and it is likewise true that all dogs are mammals, then it must be true that all dogs are warm blooded. In some sense we might say that “the truth” of the conclusion is “contained in”” the truth” of the premises. Moreover, since it is in fact true (or so we believe) that “all mammals are warm blooded” and “all dogs are mammals,” it must be in fact true that “all dogs are warm blooded.”

It is important to see that there are two notions at work here: an “if--then” or “hypothetical notion” and a straightforward “factual” or “truth notion.” If it is true that “mammals are warm blooded” and “dogs are mammals,” then it must be true that “dogs are warm blooded.” This is the hypothetical claim: if one set of claims -- the premises -- are true, then so is the other -- the conclusion. But this “hypothetical claim” does not make the straightforward claim that either premises or conclusion is true. If we do make the “hypothetical claim,” however, and in addition claim that the premises are in fact true, this gives us license to claim that the conclusion is also in fact true.

In illustration of this distinction between “hypothetical” and “factual,” consider the following argument and diagram.

EX. 4-1-c

All reptiles are warm blooded creatures.
All fish are reptiles.
-------------------
All fish are warm blooded creatures.

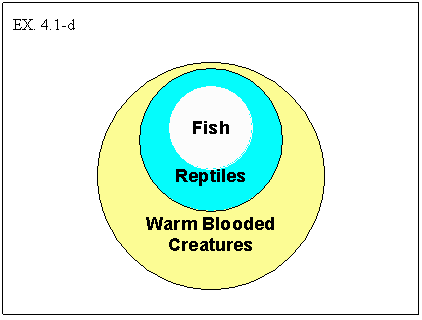
Here, as with our first argument, if it is true that “all reptiles are warm blooded” and “all fish are reptiles,” then it must be true that “all fish are warm blooded.” Again, there is a sense in which all of the logical information expressed by the premises includes the logical information expressed by the conclusion (the truth of the premises contains the truth of the conclusion). The particular “if--then” structure of the argument guarantees this. When a deductive argument has such a structure we say that it is valid.

A valid argument is an argument of such a form that if the premises are true, the conclusion must be true.

Both our “dog” and “fish” arguments are valid and indeed they are instances of the very same valid argument form. Here it is:

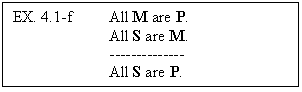
Here ‘S’, ‘P’, and ‘M’ function as kinds of “variables” that can take on different “values” in particular arguments. In accord with a long tradition, we use ‘S’ to refer to the “subject term” of the conclusion, ‘P’ to refer to the “predicate term of the conclusion” and ‘M’ to refer to the “middle term” that appears in each of the premises. We say more about this in section 4.2.

Returning to our “dog” (4.1-a-b) and “fish” (4.1-c-d) arguments, clearly one of these arguments is “better” than the other and this is because it not only has a “good if--then structure,” but also it has premises that are “factual.” That is, the premises of our “dog” argument are in fact true rather than false and thus we say it is not only valid but also sound.

Sound arguments are valid arguments with all true premises. That is, a sound argument (1) is a valid argument and (2) has all true premises

So we have outlined two important notions of what counts as a “good deductive argument.” “Validity” has to do with the “form,” or “if--then structure” of the argument. If the structure guarantees that “if the premises are true, then the conclusion must be true,” then the argument is valid. If in addition to having such a “valid structure” an argument has all true premises, then the argument is sound. Thus, “soundness” has to do with both “structure” and “content” and sound arguments are deductive arguments of the “highest quality.”

But of course deductive arguments can fail to be valid and thus likewise fail to be sound. Consider the following:

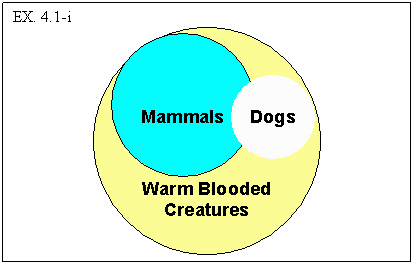
If, as the diagram depicts, it is true that both mammals and dogs are “warm blooded,” this by itself does not allow us to infer that it must be true that “all dogs are mammals.” We know that they are but the “structure of the argument” does not guarantee this. This is an invalid argument since it is not an argument of such a form that the truth of the premises guarantees the truth of the conclusion. Note too that despite the fact that all of the premises as well as the conclusion of this argument are in fact true, because the argument is invalid, it is also unsound. Sound deductive arguments are ones where true conclusions are conclusively inferable from true premises. If either “guaranteed inferability” or “true premises” is lacking, then the argument is unsound.

4.2 Deductive Logic -- Aristotle’s Square

Over 2000 years ago the Greek philosopher Aristotle wrote a series of works, known collectively as the Organon, in which he laid the foundations for all of what we currently understand as reasoning or logic. In particular, Aristotle’s account of deductive logic continues to be employed today. What follows in this section and the next is a brief exposition of some of the useful highlights that have grown from Aristotle’s account.

We begin with what has come to be called “Aristotle’s Square of Opposition.” The “Square,” depicted below, illustrates some of the “truth-relations” that Aristotle found to hold among various kinds of statements. The four primary kinds of statements he considers were later given the “nicknames” of ‘A’, ‘E’, ‘I’, and ‘O’ and as a group have come to be called categorical statement-kinds.

Each of these statement-kinds points to a relation between two particular kinds or classes of things, an “S” or subject-kind and a “P” or predicate kind. Moreover, each statement kind is said to have a quantity and a quality. Quantity is said to be either universal or particular. A and E statement-kinds are said to be universal in quantity in that they say something about “all members of a kind or class.” I and O statement-kinds are particular in quantity since they aim to say something merely about “some (at least one) member of a kind or class.” A and I statement-kinds are affirmative in quality since they say something “positive” while E and O statement-kinds are negative in quality since they “deny” something. (Indeed, the nicknames ‘A’, ‘I’, ‘E’, and ‘O’ were taken from the first two vowels of each of the two Latin terms ‘affirmo’ and ‘nego’.) Thus we can identify each statement-kind in terms of its quantity and quality as follows: A = universal affirmative; E = universal negative; I = particular affirmative; O = particular negative.

Here is Aristotle’s Square of Opposition:

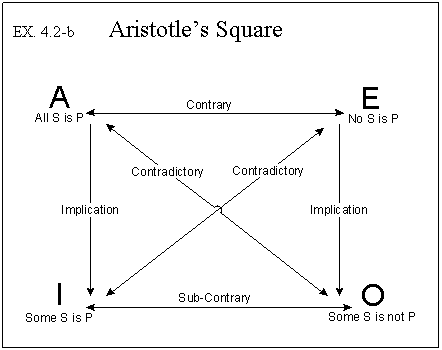
Working with only the four statement-kinds A, E, I, and O, Aristotle identifies some important “truth-relations” existing between the statement-kinds. If it is true that All S is P (All salamanders are pink), then it must be false that No S is P (No salamanders are pink). However, if it is false that All S is P, then we cannot determine the truth of No S is P. (That is, if we have some salamanders slithering around on the table and it’s false that “all of them are pink,” we can’t tell from this alone whether none of them are pink or whether some are and some aren’t.) Thus, while statements of kind A and E can’t be true together, they can be false together. This is what we call the contrary relation. “Contraries” can’t both be true but they can both be false.

Statements of kinds A and O as well as statements of kinds E and I are contradictories. They must have “opposite truth values.” Thus if it is true that “some salamanders on the table are pink,” then it must be false that “none of them are pink” and if there are salamanders slithering on the table and it is false that “some of them are pink,” then it must be true that “none of them are pink.” Analogous claims hold true for statements of kinds A and O.

The relationship of implication holds between Aristotelian statements of kind A and corresponding statements of kind I and implication also holds between corresponding E and I statements. If there are salamanders on the table and it is true that “all of them are pink,” then it must be true that “some (at least one) of them are pink.” Similarly, if a survey of the salamanders reveals that “none of them are pink,” that is, E is true, then it must likewise be true that O, “some of them are not pink.” Implication, however, is a “one-way relation.” While the truth of A statements imply the truth of corresponding I statements, the truth of I statements does not imply the truth of A statements. That is, the fact that some salamanders on the table are pink does not imply that all of them are. Likewise for O and E statements.

Interestingly, however, we learn from Aristotle’s Square that if I statements are false, then corresponding A statements must also be false. Similarly for O and E statements. We can prove this using the Square as follows:

1. If I is false, then E must be true -- Why? They are contradictories.

2. But if E is true, then A must be false -- Why? E and A are contraries.
--------------------------------------------------------------------------------
3. If I is false, then A is false.

Finally, we point to the sub-contrary relation that holds between statements of kind I and O. Here Aristotle identifies the fact that if there are salamanders on our table, then while it is easy to see how it can be true that both some are pink (I), and some are not (O), it is impossible that both of these statements are false. Thus, while statements of kinds I and O can be true together, they cannot be false together. This is the sub-contrary relation.

It is worth noting some additional truth-relations between the four statement kinds that do not appear on the Square. But, in order to identify them, we must first understand the distinction between a kind or class and its complement. Straightforwardly, we say that the class S of salamanders includes all of the salamanders that exist. The complement of S is the class non-S or S (we say “S-bar”). S is the class that includes everything in the World that is not a salamander. (This includes you, me, the Atlantic Ocean, the door knob on your bedroom … everything that is not a salamander.)

Given this understanding of a class and its complement, we can perform certain operations on categorical statements (A, E, I and O) and look to see what truth-relations the “changed statements” bear to the originals. We begin with the operation obversion. To obtain the obverse of a given categorical statement, we:

1. Change the quality of the given statement to its opposite (affirmative to negative or negative to affirmative);

2. Substitute for the term in the 2nd position (“P” or “predicate position”) its complement.

So, for example:

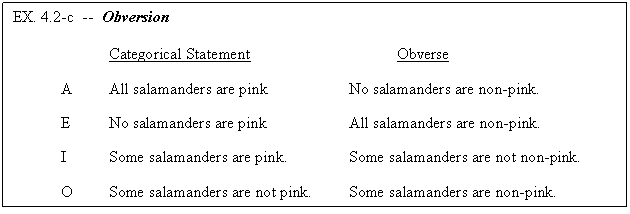
A quick inspection shows that each categorical statement is logically equivalent to its obverse. That is, if the statement is true, then so is its obverse and if the statement is false its obverse is false as well. Thus, logically equivalent statements have the same truth value and performing the operation of obversion on a categorical statement (A, E, I, or O) yields a logically equivalent statement.

A second important operation is conversion. To obtain the converse of a given categorical statement, we merely switch the terms that are in the 1st or subject position with those in the 2nd or predicate position. Thus:

Are any of these categorical statements logically equivalent to their respective converse statements? Clearly it does not follow that if it is true that all salamanders are pink, then it is also true that all pink things are salamanders! It is easy for us to imagine a world where not only all of the salamanders are pink but there are many other pink things (roses, flamingoes …) as well. We can quickly see that conversion fails to yield logically equivalent statements when performed on A and O statements. (Think for yourself about the conversion of the above O statement and why it need not have the same truth value as its converse.)

But conversion does yield logically equivalent statements when performed on E and I statements. From a logical standpoint it makes no difference whether we say that “No salamanders are pink” or whether we say that “No pink things are salamanders.” Similarly, “Some salamanders are pink” is logically equivalent to “Some pink things are salamanders.” So we say “conversion works for E and I” but “conversion fails for A and O.”

Finally, one more useful operation that we can perform on categorical statements, contraposition. To obtain the contrapositive of a given categorical statement, we:

1. Switch the terms in the subject and predicate positions;

2. Substitute for each its complement.

While this is not as easy to figure out as the converse and obverse relations above, it turns out that the contraposition operation when performed on A and O statements does in fact yield logically equivalent expressions. It fails, however, when performed on E and I statements.

To sum up, Aristotle’s Square and his further investigations of truth-relations that hold between various categorical statements provide important starting points for constructing systems of deductive reasoning that allow us to test the validity of certain kinds of deductive arguments. However, it is important to see that in this section we have already been discussing various forms of valid deductive arguments. When we say, for example, that an A statement is logically equivalent to its contrapositive, part of what we are claiming is that the following is a valid argument:

All S is P
----------------------
All non-P is non-S

But there is much more to be said about valid reasoning based on Aristotle’s Square and to a brief account of what has come to be called Aristotelian Syllogistic Logic, we now turn.

4.3 Deductive Reasoning -- Aristotle’s Syllogistic Logic

Consider a simple argument:

Based on Aristotle’s work, this is an example of what today we call a Standard Form Categorical Syllogism. This needs some explaining.

First, the above argument is a syllogism. This means simply that it is an argument with two premises and a conclusion. Second, it is a categorical syllogism. As such it is a syllogism that employs only categorical statements -- A, E, I, and O kinds of statements from Aristotle’s Square. Finally, it has standard form. That is, it is a categorical syllogism that:

Surprisingly, perhaps, it turns out that this definition allows us to identify exactly 256 varieties of standard form categorical syllogism many of which continue to be among the most commonly employed arguments today.

We identify these 256 syllogistic forms in terms of what we call mood and figure. First, a SFCS (standard-form categorical syllogism) has a mood that is nothing more than a listing from top to bottom of the kinds of categorical statements that compose the argument. In our example above, each premise as well as the conclusion of the argument is an A-type categorical statement. Thus the mood of this argument is AAA. But in addition to mood, SFCSs can also differ as regards the arrangements of the terms in the argument. There are four possible arrangements or figures.

Figure 1

M P
S M
----
S P

Figure 2

P M
S M
----
S P

Figure 3

M P
M S
----
S P

Figure 4

P M
M S
----
S P

If we look at our example 4.3-a we see that it is figure 1. Thus we say that the above argument is an AAA-1 standard form categorical syllogism. Each SFCS has four possible kinds of categorical statement (A, E, I, or O) that can occur in each premise or conclusion and in addition it has a figure. Thus, there are 4 x 4 x 4 x 4 = 256 possible varieties of SFCS.

Let’s look at another of the 256 varieties of SFCSs, an OAO-3.

EX 4.3-d

Some of My favorite things are not Pink things
All of My favorite things are Salamanders
-----------------------------------------
Some Salamanders are not Pink

Here the first premise of the argument (containing the P or predicate term of the conclusion) is an O statement, the second premise is an A statement and the conclusion is again an O statement. Hence, the mood of the argument is OAO. If we look at the arrangement of the M or middle terms we see that the figure of the argument is figure 3 or 3rd figure. Thus, this argument has the form of an OAO-3 SFCS.
But while Aristotle’s work provides a basis for distinguishing certain common varieties of syllogistic arguments, none of this by itself helps us to determine whether these arguments are “good arguments.” That is, how do we know which of these 256 syllogistic forms will be the forms of valid arguments and which ones won’t?

If we had been studying Aristotelian logic in Europe 1000 years ago, the next step in our instruction would be to learn a Latin poem that listed all of the valid argument forms from the 256. Just for fun, here is the first line of the poem: “Barbara, Celarent, Darii, Ferioque prioris.” What we have here are a series of Latin names that were chosen so that the first three vowels of each name spelled out the mood of a valid first figure (“prioris”) argument -- AAA-1, EAE-1, AII-1, EIO-1. Through intuition, inspection and argument, Aristotle and his followers found which of the 256 argument forms were valid forms and students merely took their word for it and learned the poem. (In some respects, not too different from what students are often asked to do today!)

But let’s try to determine the validity of these kinds of arguments in a more intuitive fashion by using diagrams. Consider first how we might try to diagram the logical information in simple categorical statements.

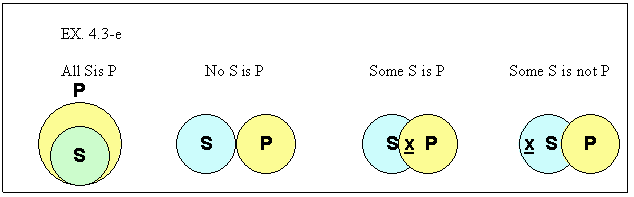
For A statements, everything that is in S is also in P. For E statements, there is no overlap between S and P. I statements say that there is some x that is found in both of S and P while O statements say that there is some x to be found in S that is not in P.

Diagrams for SFCSs, however, are more complicated since there are three terms that must be considered. We will begin all of our SFCS diagrams with a rectangle to symbolize the M or middle term. Given this, let’s consider “Barbara,” an AAA-1, probably the most common valid form of SFCS.

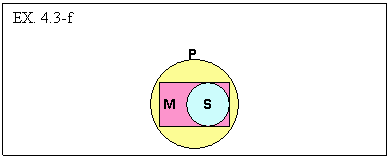
Looking back at EX. 4.3-a, we begin our diagram by drawing a rectangle to symbolize the M-kind or class “My favorite things.” Next we look at the first premise of the argument which says that “All of My favorite things are Pink” (All M is P). To symbolize this we circumscribe the M rectangle with the P circle. Next, we diagram our second premise “All salamanders are among My favorite things” (All S is M) by placing the S circle inside of the M rectangle. Thus we have diagramed both of our premises and our diagram is complete.

But now comes an inspection of the diagram in accord with the “key principle” on which this process for determining the validity of arguments depends. Here is the “key principle:”

Given this, after diagramming the premises of an argument as above, if the argument is valid, we should expect to see the conclusion already diagrammed. The conclusion of the argument under consideration is “All Salamanders are Pink.” Is this categorical statement already diagrammed? Yes, the “S-circle” is inside of the “P-circle” in our diagram and thus this AAA-1 SFCS, and, indeed, any argument having the AAA-1 form, is a valid argument.

Here is a diagram we might give for the invalid AAA-2 argument expressed in EX. 4.1-f.

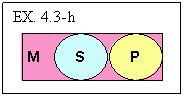
The first premise is “All mammals are warm blooded” (All P is M), and thus we inscribe the P circle in the M rectangle. For the second premise, “All dogs are mammals” (All S is M) we must do the same for the S circle but the difficulty is we have no information about how the S and P kinds are related. Hence we assume as little as possible. That is, we assume they are wholly distinct and thus No S is P. Given that we have diagrammed the premises, we now look to see whether the conclusion is satisfied. The conclusion, “All dogs are mammals” (All S is P), is not already depicted in the diagram and hence this AAA-2 SFCS is invalid. (And again, any SFCS having this form is invalid.)

We conclude this section with one more diagram based on the OAO-3 SFCS from EX. 4.3-d.

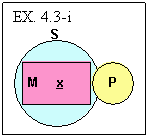
We know that to diagram our first premise, “Some of My favorite things are not Pink” (Some M is not P), we must put an x in the M rectangle that is not in the P circle. The problem is again that we do not know how to situate the P circle in the diagram. Again our solution is to suppose that the M rectangle and the P circle have nothing in common, they are wholly distinct. To diagram the second premise, “All of My favorite things are Salamanders” (All M is S) we circumscribe the M rectangle with the S circle. We now look to see whether our conclusion is satisfied and, yes, there is depicted in the diagram something that is an S but not a P and hence our argument is valid.

There are many discussions of more complete and comprehensive accounts of diagramming techniques for determining the validity of SFCSs. For our purposes it is enough to see that this is possible and that validity can most often be ascertained in a reasonably intuitive fashion. In the next two sections we look at a different variety of deductive reasoning along with some new techniques for determining validity.

4.4 Deductive Reasoning -- Sentence Connectives and Truth Tables

The logic that grows from Aristotle’s work is a deductive logic that is based on the relations that hold between kinds or classes. But in the generations that followed Aristotle, there appeared a kind of deductive logic that was formulated not in terms of classes but rather in terms of the relations between sentences (‘propositions’ was the technical term). Eventually, through the work of nineteenth century logicians G. Frege, C. S. Peirce, and others, this sentential logic developed into our contemporary symbolic logic. But while contemporary symbolic logic can be quite complicated, the essence of sentential logic is not, and, indeed, sentential logic retains a practical usefulness that is at least equal to its Aristotelian cousin. We lay the groundwork for sentential logic in this section and complete our short introduction in the next.

What is this essence of sentential logic? Simply it is the fact that most all natural languages (English, Chinese, Swahili, etc.) either explicitly or implicitly have special sentence connectives -- words/techniques for joining sentences together -- that are truth-functional. And, truth-functional sentence connectives are those that allow us to calculate the truth values of the new “complex sentence” that is produced based on the truth values of the simpler sentences on which the truth-functional sentence connectives operate (join).

Sounds complicated but some examples should help. Consider two “simple sentences:”

p: SpongeBob is here.

q: Sandy Cheeks is here.

Now suppose it is true that “SpongeBob is here” and suppose it is also true that “Sandy Cheeks is here.” Given this, what is the truth value of the complex sentence “SpongeBob is here and Sandy Cheeks is here”? Obviously it is true. We understand that for any sentences ‘P’ and ‘Q’, if ‘P’ is true and ‘Q’ is true, then it is likewise true that ‘P and Q’. Moreover, we also understand that if either ‘P’ is false or ‘Q’ is false, then the complex sentence ‘P and Q’ is also false. We can chart this feature of the truth-functional sentence connective ‘and’ in the following truth table:

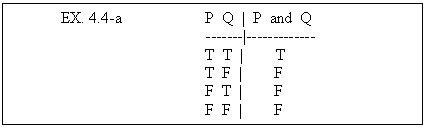
On the left hand side of the truth table we have listed the possible combinations of “truth and falsity” that ‘P’ and ‘Q’ can take on. On the first line of the truth table, both ‘P’ and ‘Q’ are true, on the second ‘P’ is true and ‘Q’ false, on the third ‘P’ is false and ‘Q’ true and on the fourth line both are false.) The complex sentence form ‘P and Q’ is true only on the first line of the truth table. On lines 2, 3, and 4, ‘P and Q’ is false.

It is traditional in sentential logic to identify five truth functional sentence connectives.

Here are the truth tables for each of these five connectives.

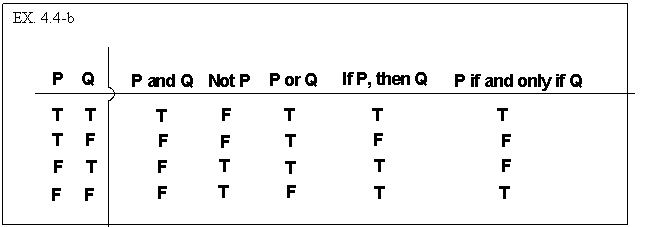
Following the truth table for ‘P and Q’ we come to ‘Not P’ or, to state its longer version, ‘It is not the case that P’. In this case the “sentence connective” ‘Not’ operates on just one sentence and it reverses the truth value of the sentence on which it operates. The truth table for ‘P or Q’ captures the ordinary language notion of “one or the other or both.” We can capture the “exclusive or” that says “one or the other but not both,” with the complex sentence ‘(P or Q) and (Not (P and Q))’.

We stated above that sentential logic is based on the fact that natural languages have truth-functional sentence connectives. So far, the match-up between “ordinary language” and the truth tables has been reasonably straightforward. Not so, however, for the sentence connective “If __, then __.” “Yes,” if we consider the first two lines of the truth table (line one, when ‘P’ and ‘Q’ are both true and line two, when ‘P’ is true and ‘Q’ is false), it does seem to agree with our common sense understanding of “If P, then Q.” However, lines three and four are a puzzle. In ordinary language, we are not quite sure what to say when the “if-part” of the “if __, then __” is false. But in order to avoid gaps in our truth tables we interpret “If P, then Q” as expressing the claim “It is not the case that both P is true and Q is false. Thus we claim that the truth table for “If P, then Q” is identical to the following:

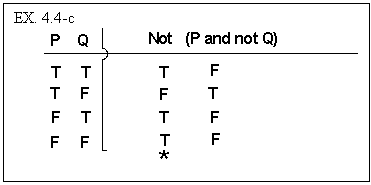
For example, when we say that “If SpongeBob is here, then Sandy Cheeks is here,” we claim that this is equivalent to saying that “It is not the case that both SpongeBob is here and Sandy Cheeks isn’t.”

The final truth-functional sentence connective that is traditionally discussed is the less often employed “if and only if.” We interpret this as saying “If P, then Q AND If Q, then P.” The upshot of this is that if we join simpler sentences by means of the connective “if and only if,” the resulting complex sentence will be true whenever the two simpler sentences have the same truth value and it will be false when they do not.

4.5 Deductive Reasoning -- Sentential Logic

Thus far we have introduced the foundations of sentential logic but we have yet to show how we can employ these foundations to test for the validity of arguments. In this section we remedy this lack and in the process look at some of the most common forms of valid arguments expressed in terms of sentential logic.

We begin with what is probably “the” most common valid argument form expressed in ordinary language, modus ponens (the “mode of putting” the truth of the first part (antecedent) of the “if __, then __”). Here is an oft’ used example: If it is raining, then the streets are wet. It is raining. Therefore, the streets are wet. If we make “sentence assignments” as follows:

p: It is raining.

q: The streets are wet.

then we can symbolize this argument as:

If p, then q
p
-------------
q

Most people will intuitively conclude that this is a valid argument. That is, they “see” that this is an argument of such a form that if the premises are true, then the conclusion must be true. Now, however, we can employ the truth tables discussed in the previous section to “prove” that this is in fact a valid argument. Here is the proof:

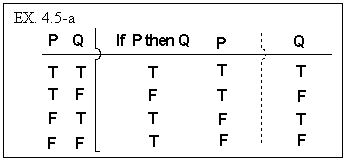
We give the truth tables of each of the premises, “If P, then Q’, and ‘P’ and we follow this by giving the truth table of ‘Q’. Note that when we give the truth tables of ‘P’ and ‘Q’, we are merely repeating the initial assignments of truth and falsity to ‘P’ and ‘Q’ that we employ to generate truth tables.

We are now in a position to judge whether the argument we have symbolized is valid. First, remember that in sentential logic we employ truth-functional sentence connectives that allow us to calculate the truth values that complex sentences take on based on the truth values of their simpler-sentence-parts. Because we consider all possible combinations that the “simpler parts” can take on, this in turn allows us to give a complete accounting of the truth values of the truth-functionally-connected complex sentences in which they participate. Thus, by giving truth tables of the premises and conclusion of an argument in sentential logic, we can look to see whether there is any initial assignment of truth/falsity that makes each of the premises of the argument true and the conclusion false. IF THERE ARE NO ASSIGNMENTS THAT MAKE EACH OF THE PREMISES TRUE AND THE CONCLUSION FALSE, THEN (since we have considered all of the possibilities) THE ARGUMENT IS TRUTH-FUNCTIONALLY VALID. For modus ponens, since there is no assignment of truth values to ‘P’ and ‘Q’ (no line on the truth table) that makes the premises ‘If P, then Q’ and ‘P’ both true, and the conclusion ‘Q’ false, we have shown that this is a valid argument form and that any particular argument that has this form is valid.

Compare this with an intuitively invalid argument: If it is raining, then the streets are wet. The streets are wet. Therefore, it is raining. In symbols:

If p, then q
q
-------------
p

With a bit of thought we see that it is possible that both premises of this argument are true and yet the conclusion is false. (The streets may become wet because of a leaky hydrant.) Hence, the argument is invalid. Here is the proof.

Inspection reveals that in the list of initial assignments to ‘P’ and ‘Q’, when ‘P’ is false and ‘Q’ is true (third line of the truth table), each of the premises of the argument is true while the conclusion is false. THIS IS IMPOSSIBLE FOR A VALID ARGUMENT and hence this argument is invalid. (Indeed, we say that this argument commits the logical fallacy of “affirming the consequent” (consequent -- second or “then-part” of the “If __, then __”).

We conclude this section with a brief catalogue of some of the most common valid argument forms (in addition to modus ponens) that we employ in our ordinary, everyday reasoning. We leave it to the interested reader to employ truth table techniques to prove that these argument forms are valid.

Modus tollens (the “mode of taking” away the truth of the “then-part” of the “if __, then __”): If it is raining, then the streets are wet. The streets aren’t wet. Therefore, it’s not raining.

If p, then q
Not q
-------------
Not p

Hypothetical Syllogism. Note that arguments often contain more than two simple sentences and this entails that there are more combinations of truth and falsity that must be considered in a truth table representation of the argument. (For three simple sentences, eight combinations of truth/falsity; four simple sentences, sixteen combinations; N simple sentences, 2N combinations.) Here is an example of a hypothetical syllogism: If SpongeBob is here, then Sandy Cheeks is here. If Sandy Cheeks is here, then Squidward is here. Therefore, if SpongeBob is here, then Squidward is here.

If p, then q
If q, then r
-------------
If p, then r

Disjunctive Syllogism. Either SpongeBob is here or Sandy Cheeks is here. Sandy Cheeks isn’t here. Therefore, SpongeBob is here.

p or q
Not q
-------------
p

Dilemma. SpongeBob is here or Squidward is here. If SpongeBob is here, then Sandy Cheeks is here. If Squidward is here, then Patrick Starfish is here. Therefore, either Sandy Cheeks is here or Patrick Starfish is here.

p or q
If p, then r
If q, then s
-------------
r or s

Reductio ad absurdum. This is a kind of valid deductive argument that sounds unusual but is actually quite common. We often argue as follows: “If what you say is true, then something “completely nutso” follows. Therefore, what you say must be false.” In formal logic, the “most nutso” claim one might make is a “self contradictory statement,” a statement that must be false. In sentential logic, the most common form of such a statement is “P and not P.” Thus the sentential logic version of reductio ad absurdum might look like this.

p
If p, then (q and not q)
q and not q
-------------
Not p

Note that in sentential (formal) logic, “anything and everything” follows from a contradiction. This is because if there is a self contradictory statement among the premises, then it will always be impossible for “all the premises to be true and the conclusion false.” And this is because it will always be impossible for there to be “all true premises.”

4.6 Deductive Reasoning -- Summing Up

In this Chapter we have looked at a form of reasoning employed in problem solving that has been the subject of research for well over two thousand years. Deductive reasoning is notable for its seeming precise and conclusive nature as well as the simple techniques we have developed to distinguish good deductive reasoning from bad. It is rare, however, that deductive reasoning by itself can solve any of our problems of action/reflection. More help is needed and to an account of another kind of reasoning we now turn.